February 4, 2017 10:00 pm

The Math Behind “Hidden Figures” – Why STEM is important and math is everywhere!

Today’s guest blog post is by StarTalk intern Kirk Long. Kirk is majoring in physics while minoring in mathematics and piano at Idaho State University.

I saw the movie Hidden Figures over the long weekend, and like most moviegoers I left feeling inspired and uplifted by the story of Katherine Johnson, Dorothy Vaughan, Mary Jackson, and the many other computers at NASA. I won’t spoil too much about the movie, but if you haven’t seen it yet I highly recommend it and I’ll even go so far as predicting with a pretty high level of confidence that you will enjoy it—if you’re reading this, you’re a StarTalk fan, so I think it’s safe to say a love of space and understanding how we get there is a shared interest we have.

Hidden Figures is not just a story of empowerment for women and people of color, but to a lesser extent for mathematicians. In a world of Hollywood blockbusters filled with explosions and fancy CGI, it’s really pretty cool to see a movie like Hidden Figures perform so well despite the story being dependent on a subject most Americans hate—math. In fact, one of the key moments of the film (I’ll try to focus on just the math here, so it’s not too much of a spoiler, but skip this part if you still haven’t seen it and don’t want to know anything) hinges on the work of one of math’s most famous rock stars, Leonhard Euler. To get America to the moon we needed a bigger rocket, but we also needed to start using new kinds of trajectories (before we had basically just been going straight up and hoping for the best) and we needed new kinds of math to model those trajectories. There are so many more variables in these kinds of equations, and they turned out to be very difficult to approximate to the specifications both the military and astronauts demanded—one small error in the calculations for when to slow the spacecraft down to start its descent into the atmosphere could result in it burning up, and the Navy demanded that NASA be able to bring the capsule down within a 20-mile square of ocean.

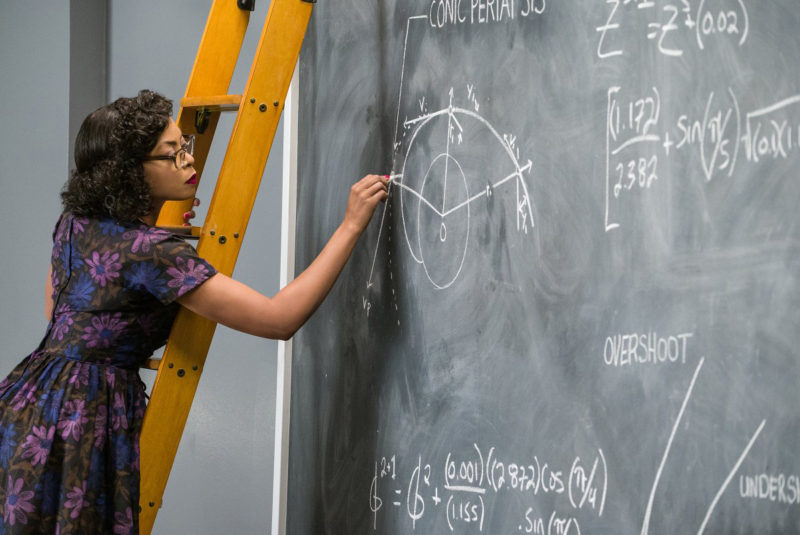
Katherine Johnson was integral to figuring out how to solve this problem, and in doing so exposes one of the reasons math is both really important and really cool. In the movie, she has a eureka moment while staring at a blackboard and realizes that “old math” might be the solution. She turns to Euler’s method, which in layman’s terms allows the mathematician to approximate a differential equation numerically without actually ever really solving it. It’s a tedious process, but this process (and others that are philosophically similar to it) are what run our computers’ math brains today—something Dorothy Vaughan helped to implement towards the end of the movie when she used the massive early IBM computer to start checking the numbers done by Johnson and other computers.

What’s most exciting to me, though, is that Johnson underscores the most fundamental reason math is important to our lives, even if you’re not a rocket scientist. Math is interconnected and intertwined in everything. Euler would have never imagined that his methods might one day be used to land men on the moon, but his techniques allowed for just that. Likewise, solving these differential equations isn’t just important to rocket scientists—they have allowed for unparalleled advances in almost every field of study, from better patient care to self-driving cars, and most of us have never given a second thought to how crazy and exciting that is.

Math really is everywhere, and you really should care about it. Training your brain in math allows you to see the connections between things you might otherwise have missed, just as Johnson does in Hidden Figures. I ran into Janna Levin last month (StarTalk All Stars Host and astrophysicist extraordinaire) and we got to talking about math (of course). I asked her what she thought was the most important equation or mathematical concept we use in everyday life (because every nerd has a favorite). Her answer was deeper than what I was expecting, however, when she said “critical thinking.” I think she’s 100% right. Perhaps that’s why math majors have the highest average scores on the both the LSAT (Law School Admissions Test) and the fourth highest average score on MCAT (Medical College Admissions Test) behind economics, physics and biomedical engineering, and why we’re so fun to talk to at parties.

“But I just don’t get math!”—Most people everywhere

Whenever I tell people I’m studying math and physics at school, this is a common phrase I hear, and it’s one that I hate. Math—like being good at anything else—requires dedication and practice, but just as anyone can become a decent writer or musician, anyone can learn to do math. Math is beautiful because it is the language that governs our universe, from the physics of exploding stars to everyday life here on Earth. If you’re already a math whiz (and many of our listeners are), then you’ve probably encountered the same stigma I have, but it doesn’t have to be that way!

The biggest reason I think math and most STEM subjects are more intimidating to outsiders than many other disciplines is that they require learning an entirely new language—that’s right, math is a language.

If you think you’re bad at math, you’re not alone. One of the first things I bring up when asked why I chose to study math and physics in college is because math has always been my worst subject, and that’s one of the reasons I love it so much. Math challenges me every day in ways that other disciplines just couldn’t, and by learning math not only am I picking up useful skills I can apply in my day-to-day life, but I’m gaining a deeper understanding into the mysteries of the cosmos—from the scales as grand as the observable universe to as miniscule as the building blocks of matter and life as we know it.

Math isn’t beyond anyone’s reach, even in advanced courses. Around 300 years ago (no calculators) Isaac Newton invented calculus by hand, basically on a dare, all before he was 26. This is a crazy feat, but think about the wealth of knowledge available at our fingertips today. Most of us will never have the level of insight and connection to the universe that Newton had, but anybody can follow in his footsteps. In many college calculus classes calculators are actually forbidden, because the actual computations are really not that hard. I love showing people that math really isn’t that scary, and I’ve taught everyone from my friends trying to get through Calculus I to second-graders in some of my science camps. One of my favorite things is seeing the lightbulb click for a future scientist when he or she realizes that math isn’t that scary or that hard after all.

Don’t believe me? Let me teach (or reteach) you what I teach those second-graders on their last day of camp. One of the most important concepts in calculus is something called a derivative. Basically, a derivative is a measure or expression of how fast something is changing. The most ubiquitous and useful trick you’ll learn in calculus to help you find derivatives is something called the power rule. I’ve outlined a basic pattern of functions (all of the f(x) equations) and their derivatives (all of the f’(x) equations) below, see if you can figure out the pattern:

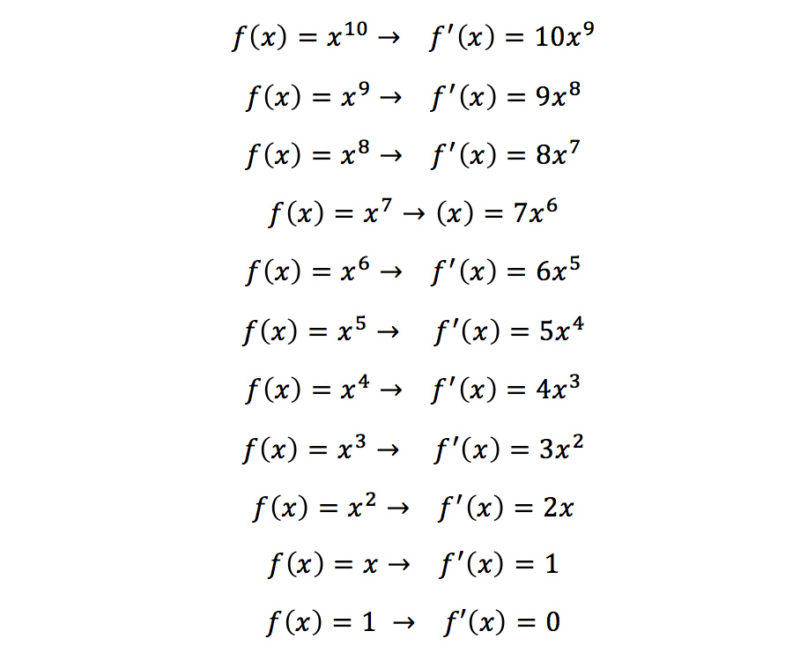
Most people get the pattern, but a lot of the time people are confused as to why the derivative of x is just 1 and why the derivative of 1 is 0. Remember, derivatives are a measure of how fast something is changing. If we just have x (as opposed to xⁿ) that means that the rate of change is constant, and thus 1. If we just have a number (like 1 at the very bottom) without any variables in the equation that means that there isn’t going to be any change at all, and the rate of change thus becomes zero (the derivative of 1,000,000,000 is also 0 because of this). Each time we take the derivative, we multiply the variable (x) by the old exponent, then replace the exponent with the number one less than the previous one. Thus, in general, we can write the equation for finding a basic derivative using the power rule like this:

If f(x) = xⁿ then f’(x) = nx^n-1

There’s a “mathier” full calculus definition that explains why this works (if you’re curious, here’s a good explainer from the Khan Academy) but this concept is applicable everywhere from accounting to rocket science—really. Derivatives are incredibly important because they allow us to approximate functions that would otherwise be too complex—this philosophical concept is exactly what Euler’s method allowed Katherine Johnson to do in Hidden Figures, although the method is more complicated than the power rule outlined above. I use the power rule (and a lot of other calculus) every day, and that puts me in the same league as scientists at NASA, engineers at Tesla, cancer researchers, architects, and so many more professions.

Math is everywhere if you care to look, and just because something seems foreign doesn’t necessarily mean it’s scary or difficult—our brains have an incredible capacity to learn. You don’t have to be a genius to understand math – you just have to be willing to give it a chance.